OTOMATA HINGGA NONDETERMINISTIK

Seperti yang sudah di bahas di materi sebelumnya,  otomata dibagi menjadi dua jenis, Deterministik (AHD) dan Nondeterministik (AHN). Dan jika dilihat dari isi tabelnya, jelas terlihat perbedaan dari AHD dan AHN. Berikut datailnya :

Otomata Hingga Deterministik (AHD)

Fungsi Transisi akibat pembacaan sebuah simbol bersifat tertentu, artinya
- Setiap cell hanya terdapat satu (1) digit stata tujuan
- Setiap stata terdapat busur panah keluar sebanyak input yang ada

Otomata Hingga Nondeterministik (AHN)

Fungsi Transisi akibat pembacaan sebuah simbol bersifat tertentu, artinya
- Setiap cell dapat berisi nol, satu bahkan lebih dari satu digit
- Setiap stata boleh terdapat busur panah dengan input yang sama, namun tujuan yang berbeda.


EQUIVALENSI AHN MENJADI AHD

Bentuk Otomata Nondeterministik dapat diubah menjadi bentuk Deterministik tanpa mengubah arti.
Berikut Algoritmanya :
1. Tetapkan Stata awal AHD = Stata awal AHN atau selanjutnya ditulis S(AHD) = S(AHN)
2. Tetapkan Input AHD = Input AHN atau selanjutnya ditulis V(AHD) = V(AHN)
3. Copykan tabel AHN sebagai tabel AHD, mula-mula Stata AHD = Stata AHN atau selanjutnya ditulis K(AHD) = K(AHN) dan Fungsi transisi AHD = Fungsi transisi AHN atau selanjutnya ditulis M(AHD) = M(AHN)
4. Setiap stata yang merupakan nilai dari fungsi M(AHN) namun stata tersebut bukan elemen dari K(AHN), maka tetapkanlah sebagai elemen baru dari K(AHD). Tempatkan stata tersebut pada kolom stata M(AHD). Lakukan pemetaan sesuai berdasarkan fungsi M(AHN).
5. Ulangi langkah 4 hingga tidak diperoleh stata baru.
6. Stata Penerima AHD atau selanjutnya ditulis Z(AHD) adalah semua stata yang mengandung stata elemen Z(AHN).

Contoh Soal :
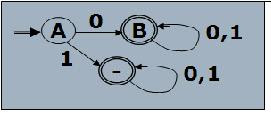
Buatlah AHD yang equivalen dengan AHN berikut :

Jawab :

1. S(AHN) = S(AHD) = A

2. V(AHN) = V(AHD) = {0,1}

3. Copykan tabel AHN

4. Simbol - dianggap sebagai elemen baru, kemudian petakan berdasarkan fungsi M(AHN).
5 karena tidak ada pengulangan makan lanjutkan ke langkah berikutnya.
6. Z(AHD) = Z(AHN) = {B} karena tidak ada lagi elemen baru yang mengandung elemen Z(AHN).

dan hasilnya adalah :

FINITE STATE AUTOMATA

Finite State Automata atau Otomata Hingga dikemukakan McCulloch dan Pitts (1940) untuk memodelkan neuron nets, dan juga digunakan untuk merancang switcing circuit.

Otomata Hingga dapat dinyatakan sebagai pengenal bahasa, bahasa yang dikenali adalah bahasa sederhana namun mempunyai aspek penerapan sangat penting di ilmu informatika / komputer, yaitu bahasa Regular, yang didefinisikan sebagai pasangan 5 tupel, yaitu :
K = Himpunan Stata, digambarkan dengan lambang lingkaran
V = Himpunan Input, label yang terdapat pada panah transisi
S = Stata awal, yang ditandai dengan gambar panah di depan stata
M = Fungsi Transisi, memetakan Stata dengan inputnya menuju ke stata tujuan.
Fungsi Transisi dapat disajikan dalam bentuk tabel transisi atau diilustrasikan
dalam bentuk graf
Z = Himpunan Stata Penerima, yang ditandai lingkaran ganda, apabila tracing input berhenti di salah satu stata penerima maka kalimat tersebut dikenali oleh mesin tersebut

Otomata Hingga dibagi menjadi 2 jenis, yaitu :
- Otomata Hingga Deterministik (Deterministic Finite Automata)
- Otomata Hingga Nondeterministik (Nondeterministic Finite Automata)

Otomata Hingga yang biasa digunakan dalam hal ini merupakan Otomata Hingga Deterministik, untuk yang lainnya akan disebutkan secara lengkap namanya.

Jika ada dua buah mesin OTOMATA hingga yang mana keduanya sama-sama dapat menerima atau mengenali bahasa yang sama, maka keduanya dapat dikatakan equivalen. Namun untuk lebih jelasnya ada algoritma yang mengaturnya, yaitu :
1. Pastikan nama stata pada kedua otomata hingga tersebut berbeda (tidak sama).
2. Buat tabel antara pasangan stata (stata AHD1, stata AHD2) dengan input-inputnya
3. Pasangan stata pertama diisi dengan stata awal masing-masing AHD
4. Perhatikan nilai-nilai pasangan stata pada baris pertama, apakah ada pasangan stata baru
yang belum terdaftar di kolom stata? jika ada, tempatkan pasangan stata tersebut sebagai
pasangan stata baru, kemudian lakukan sesuai aturan fungsi transisinya.
5. Lakukan langkah ke-4 sampai tidak ditemukannya pasangan stata baru. Dan kedua AHD
tersebut dinyatakan equivalen atau sama-sama dapat menerima bahasa yang sama.

Contoh :
1. Jika diketahui :
K = {A, B}, V = { a }, S = A, Z = { B }
M(A, a) = B
M(B, a) = A
- Gambarkan grafnya
- Tentukan bahasa yang dihasilkan, L(G)?

2. Jika diketahui :
K = {A, B}, V = { a }, S = A, Z = { B }
M(A, a) = B
M(B, a) = B
- Gambarkan grafnya & Tentukan L(G) nya

3. Apakah kedua otomata hinggga diatas equivalen? Buktikan!

NFA with ^ move

AHN with ^ atau biasa ditulis AHN-^ merupakan jenis otomata baru, artinya otomata ini dapat berpindah stata tanpa membaca input.

Seperti pada gambar mesin otomata di atas, stata q0 tanpa membaca input dapat berpindah ke stata q1, begitu pula q1. Stata q1 tanpa membaca input dapat berpindah ke q2.

Seperti yang sudah dijelaskan, bahwa AHN-^ dapat dibuat AHN yang ekivalen, dengan demikian dapat pula dibuat AHD yang ekivalen.

Untuk mengubah AHN-^ yang ekivalen dengan AHN, harus mencari nilai ^- Closure setiap stata. Apakah ^- Closure(stata) itu?

^- Closure suatu stata atau biasa ditulis ^- Cl(stata) adalah himpunan stata-stata yang dapat dicapai dari suatu stata tanpa membaca input.

Dari gambar mesin otomata di atas dapat diperoleh :
^- Cl(q0) = {q0, q1}
^- Cl(q1) = {q1, q2}
^- Cl(q2) = {q2}

EQUIVALENSI AHN-ε ke AHN

Untuk memudahkan kita mencari ekivalensi AHN dari AHN-^, gunakanlah Algoritma atau langkah-langkah sebagai berikut :

1. Tentukan ^ - closurenya
2. Buat tabel transisi AHN-^
3. Carilah setiap fungsi transisi hasil perubahan dari AHN-^ ke AHN dengan rumus berikut: M(Stata,Input) = ^-Cl (M(^-Cl(Stata),input) )
4. Berdasarkan hasil no 3, buatlah tabel transisi dan diagram transisinya
5. Stata penerimanya Z(AHN) adalah : stata penerima pada AHN-^ ditambah stata pada^-Cl yang hasilnya mengandung stata penerima pada AHN-^